Cardinal de un conjunto.

significa también, numero de elementos del conjunto.
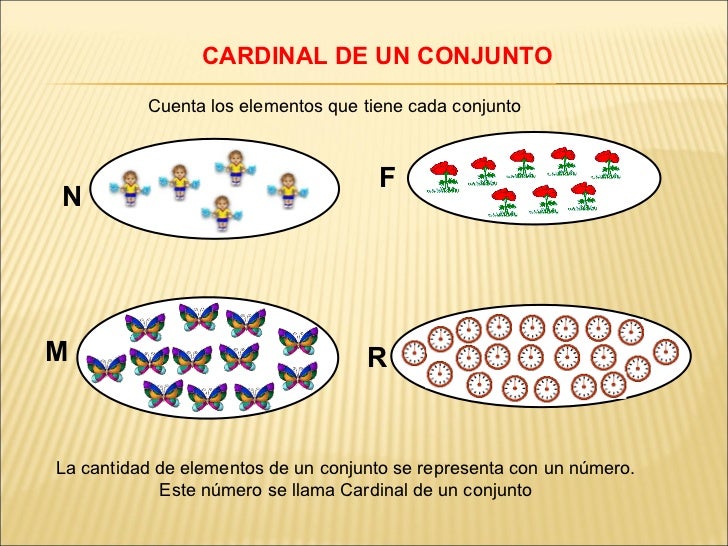
osea el cardinales el numero de elementos que posee. El cardinal de un conjunto A se denomina por n(A) y se lee; "numero de elementos del conjunto A."
 Es la unión de dos conjuntos se define como la suma de los cardinales de los conjuntos, menos el cardinal de la intersección.

n(A u B) = n(A) + n(B) -n(A n B)

Aplicaciones de las operaciones.

Teoría de conjuntos.

es una colección de objetos bien definidos por medio de alguna o algunas propiedades en común. Por objeto entendemos no solo cosas físicas, sino también abstractos como números, letras, etc..
un conjunto se puede escribir en cualquiera de las formas siguientes:

1. Forma tabular, enumerativa o extensiva.
2. forma descriptiva o comprensiva.
3. forma gráfica.

Variaciones de la condicional.

existen 3,

1. la reciproca. q => p
2. La inversa.  ~p => ~q
3. La contra-positiva. ~q => ~p

Condicional o Implicación.

Condicional de las proposiciones p y q es la proposición p => q(si p entonces q ), cuya tabla de valores de verdad es;

Por ejemplo;

LEYES DEL ÁLGEBRA PROPOSICIONAL, Leyes de morgan.

Las leyes de Morgan son una parte lógica proporcional y analítica creada por Augustus de Morgan (madura, 1806)(Londres, 1871).

Las leyes de Morgan son muy útiles cuando se quieren encontrar equivalentes para las proposiciones que se obtiene por negación de proposiciones compuestas.
La negación de una conjunción equivale a la disyunción de las negaciones.

~(p^q)=~p\/~q

La Negación de una disyunción equivale a la conjunción de las negaciones.

~(p\/q)=~p^~q

Conjunción y Disyunción.

• Conjunción.

Dadas dos proposiciones; p y q, se denomina conjunción a la proposición  p /\ q (se lee P y q) cuya tabla para entender es esta.

• Disyunción.

Dadas las dos proposiciones p y q, la disyunción de estas, es la proposición p \/ q cuya tabla de valor de verdad es;